Drawing polygons and stars with C# turtle graphics (and GCD calculation)
Suppose you have a fixed number of vertices. How can you connect them to a regular polygon or a star? Here we need some math: prime factorization and GCD (Greatest Common Divisor). And with Woopec C# Turtle Graphics we can then calculate and draw that.
What we want to achieve
Let’s look at an example with 8 corners. Depending on a delta, which determines the next corner to be connected, we get different figures. With delta = 1 the regular polygon is created. With delta = 3 a regular star is created.
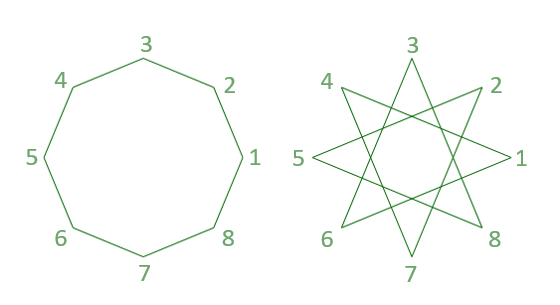
We want to write a program that draws the regular polygon and all star variants for any given number of vertices.
How many different stars with eight corners are there?
In the above example, what would happen if you worked with delta = 2 instead of delta = 3? Then you would go from corner 1 to corner 3, then to corner 5, then to corner 7, and then back to corner 1. So with a delta equal to 2, you wouldn’t go through all eight corners at all, but instead create a square. The effect that not all corners are passed through always occurs when the number of corners and the delta have a common divisor greater than 1. In this example, 8 and 2 have the common divisor 2.
For 8 vertices only the deltas that do not have a common divisor with 8 make sense. These are the values 3, 5, and 7. The deltas that are greater than 8/2 can also be ignored because they produce the same figure as a value equal to 8-delta. This means that instead of delta equal to 5, you can also work with a delta equal to 3.
So there are only two different shapes for eight corners: the polygon (delta = 1) and one star shape (with delta = 3).
But for seven corners, for example, there are two different star shapes: one with delta = 2 and the other with delta = 3.
Calculate the greatest common divisor (GCD)
To determine if vertex count and delta have a common divisor, we calculate the greatest common divisor (GCD) of the two numbers.
There are different methods to calculate the GCD. We may remember the prime factor analysis from school. This means that the two numbers are first broken down into their prime factors. The code for this looks like this:
public static Dictionary<int, int> PrimeFactorsOf(int n)
{
var highestPossibleDivisor = Math.Sqrt(n);
// At first we calculate all relevant prime numbers:
var primes = new List<int>();
for (var i = 2; i <= highestPossibleDivisor; i++)
{
if (!primes.Exists(p => i % p == 0))
primes.Add(i);
}
var primeFactors = new Dictionary<int, int>();
// Try to divide n by all prime numbers smaller than highestPossibleDivisor:
var primeIndex = 0;
var rest = n;
while (primeIndex < primes.Count() && rest != 1)
{
var prime = primes[primeIndex];
var count = 0; // how often can n be divided by prime
while (rest % prime == 0)
{
rest /= prime;
count++;
}
if (count > 0)
primeFactors.Add(prime, count);
primeIndex++;
}
// This case happens if n is a prime number
if (rest > 1)
primeFactors[rest] = 1;
return primeFactors;
}
The result of this method is a dictionary. The key of a dictionary entry is a prime number, the value of a dictionary entry is the number of times the number n can be divided by the prime number.
The greatest common divisor of two numbers a and b is the product of the common prime factors of a and b. This is calculated by the following method:
public static int GCD(int a, int b)
{
var gcd = 1;
var lowerValue = Math.Min(a, b);
var higherValue = Math.Max(a, b);
var factorsOfLowerValue = PrimeFactorsOf(lowerValue);
var factorsOfHigherValue = PrimeFactorsOf(higherValue);
foreach (var factorOfLowerValue in factorsOfLowerValue)
{
var prime = factorOfLowerValue.Key;
var countInHigher = factorsOfHigherValue.GetValueOrDefault(prime);
if (countInHigher >= 0)
{
var countInLower = factorOfLowerValue.Value;
gcd *= (int)Math.Pow(prime, Math.Min(countInLower, countInHigher));
}
}
return gcd;
}
Check the inputs
Using the GCD method above, we can validate the user input to see if it makes sense:
public static void CheckInputs(int givenCorners, int givenDelta)
{
if (givenDelta == 1)
{
// OK. This is the regular polygon
}
else
{
// Check star properties
var gcd = Fractions.GCD(givenCorners, givenDelta);
if (gcd > 1)
{
// If the given values for corners and delta have a common divisor, the resulting star has less corners.
// We can calculate the real corners and the real delta of the resulting star:
var corners = givenCorners / gcd;
var delta = givenDelta / gcd;
throw new ArgumentException($"The given values would create a star with {corners} corners and a delta of {delta}");
}
if (givenDelta > givenCorners / 2.0)
{
var delta = givenCorners - givenDelta;
throw new ArgumentException($"The given delta produces the same star as delta {delta}");
}
}
}
Draw the star
We still need some math to calculate how the turtle needs to turn and move.
For this we take this example with corners equal to 5 and delta equal to 2. The user should also be able to specify the size of the star via a radius parameter.
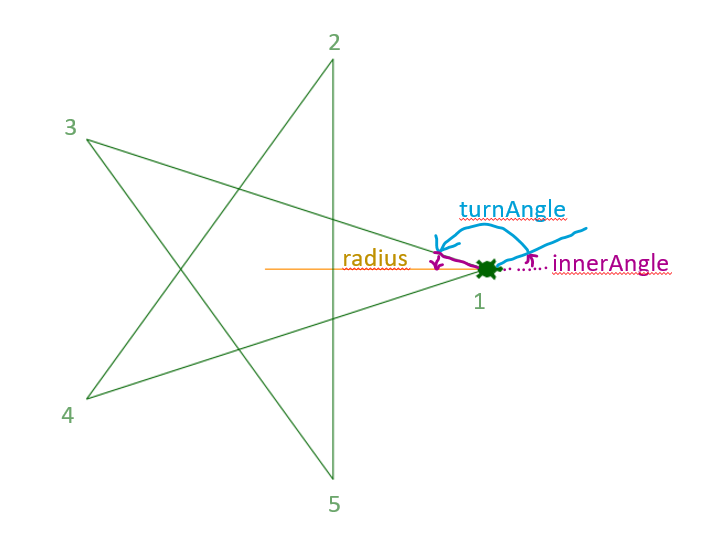
First we determine how many degrees the turtle needs to rotate at each corner. This is the turnAngle in the figure above. In order to draw all the corners, the turtle has to turn corners many times around the turnAngle. And all in all it makes delta many times a complete rotation of 360 degrees. It follows:
turnAngle = delta * 360 / corners
At the very beginning, the turtle has to turn a little bit to the left so that the first corner of the star is pointing exactly to the right. This is the innerAngle. This is simply calculated like this:
innerAngle = (180 - turnAngle) / 2
Finally we need the length, that is the distance between two corner points. In the example above, the center of the star and the vertices 1 and 3 form an isosceles triangle. The equal sides have the length of radius. We already know the equal angles in this triangle, namely innerAngle. The value forlength can then be determined from this:
length = 2 * radius * cos(innerAngleRadiant)
With these values we can implement the final drawing method:
public static void DrawStar(int corners, int delta, double radius)
{
CheckInputs(corners, delta, radius);
var turnAngle = (double)delta * 360 / corners;
var innerAngle = Math.Abs(180 - turnAngle) / 2;
var innerAngleRadiant = innerAngle / 180 * Math.PI;
var length = 2 * radius * Math.Cos(innerAngleRadiant);
var turtle = Turtle.Seymour();
turtle.PenUp();
turtle.Forward(radius);
turtle.PenDown();
turtle.Left(innerAngle);
for (var i = 0; i < corners; i++)
{
turtle.Left(turnAngle);
turtle.Forward(length);
}
turtle.Right(innerAngle);
}
So in the end, with a little bit of math, drawing a star is pretty easy. ;-)
If you want to try more complicated objects, you can draw “stars” connecting the deltan corner to the deltan+1 corner. Further information can be found on the website of Simon Plouffe (“The shape of b^n mod p”) and in a github-project by Mathias Lengler. (I came across these objects through an article by Christoph Pöppe.)
 (
(